
This is perhaps nearly as good as the Babylonian approximation, but the Egyptians did not apparently have an awareness of it as being a specific constant, this is merely the effective value of it arising from their method.įrom Archimedes there is given an approximation of $\pi$ more accurate than either the Egyptian or Babylonian, but this dates from almost 2000 years after the recorded Babylonian value.

Using $96$-gons, Archimedes obtained what is now presented as the double estimate $3\frac$ or $3.166$ repeating. He proved rigorously that the ratio of the circle to the square on its radius was the same as the ratio of the circumference to the diameter, so it could be computed both ways.Īpproximating the circumference with polygon perimeters is much simpler than approximating the circle area with polygon areas as Antiphon suggested. Archimedes perfected the method in On the Measurement of the Circle. This method was mathematically justified by Eudoxus of Cnidus using what is now called method of exhaustion, and his justification is presented in Book XII of Euclid's Elements. It consists of approximating a circle by inscribed and circumscribed polygons, and can be traced to ancient Greek orator Antiphon the Sophist.
#Who was the first to calculate pi series
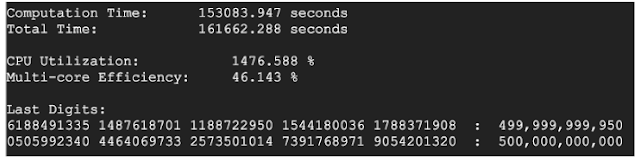
In Europe this series was rediscovered by Leibniz, and is usually called Leibniz series in Western literature.Ī semi-geometric "calculation" procedure capable in principle of producing arbitrary accuracy is much older. The first analytic formula (in the form of an infinite series) that in principle can calculate $\pi$ to any required accuracy is probably due to medieval Indian mathematician Madhava, who was first to conceive of infinite series explicitly, or one of his successors. Please enable JavaScript in your browser to complete this form.It depends on the meaning of "calculate", since $\pi$ is a transcendental number it can not be "calculated" in the usual meaning of the word. Window.FB.Event.subscribe('xfbml.render', function() (document, 'script', 'facebook-jssdk')) Emma Haruka Iwao, a Google employee who calculated more digits of pi than anyone else to this point - 31 trillion, has earned a place in the Guinness Book of World Records. Mathematicians also hoped to have more accurate calculations for pi for cosmology, though, for most pursuits, few digits are needed. The calculation of pi became a useful stress test for a computer’s abilities - almost like a test for the heart. By 1973, a million digits were reached with this method. The first time pi was computed by a machine was in 1957, when George Reitwiesner and John von Neumann used an ENIAC computer to compute 2,037 digits of pi. In modern times, endless amounts of computing power have been dedicated to approximating the infinite, irrational number to the fullest extent possible. This was suggested by William Jones, a Welsh mathematician, but not popularized until it was used by Leonhard Euler in 1737. Though pi was a well-known concept for centuries, it wasn’t until 1706 that the Greek symbol pi came to represent it.

In India, they discovered it early, between 14 A.D., yet it’s European mathematicians like Leibniz and Gregory who popularized it a century later. With the development of the infinite series (the sum of the terms of an infinite sequence) in the 16th- and 17th centuries, the way pi was calculated was revolutionized. The most correct approximation achieved using this method came in 1630, with Austrian astronomer Christoph Grienberger, who arrived at 38 correct digits of pi. This was how Archimedes first solved for pi, and it remained the dominant algorithm for pi computation for 1,000 years. Later, mathematicians attempted to better approximate pi using circumscribed and inscribed polygons. Between Zu and Archimedes, these two scientists were the first to know pi in any true sense. Since Archimedes’ books were lost, and not in China at that time, Zu calculated pi himself in a novel way. Later, in the mid-400s, another brilliant mathematician, Zu Chongzhi, computed pi again with lengthy calculations. Pi is occasionally referred to as the ‘Archimedes’ Constant.’ He found that pi fell somewhere between 3 1/7 and 3 10/71. that pi was first calculated by one of the greatest ancient mathematicians, Archimedes of Syracuse. Ancient Babylonians used it - approximated to 3.125, to calculate the dimensions of circles.

Pi has been known for nearly 4000 years in some form or another.


 0 kommentar(er)
0 kommentar(er)
